이번 포스터는 저항의 직렬 연결에서의 전압 분배, 저항의 병렬 연결에서의 전류 분배에 대해 알아보겠다!
자자 시작하겠다.
저항의 직렬 연결과 전압 분배

그림 1에서 각 저항에 걸리는 전압을 V1, V2, V3라고 정의하여 키르히호프의 전압 법칙을 구하면 아래 식이 나온다.
V1 + V2 + V3 - V = 0
V1 + V2 + V3 = V
위 식에서 우리는 각 V1, V2, V3를 풀어서 써보겠다.
V1 = R1 * i
V2 = R2 * i
V3 = R3 * i
무언가 보이지 않는가? 맞다 전류는 같고, 저항에 따라 전압이 분배되는 것을 확인 할 수 있다.
우리는 이를 통해 V = R1i + R2i + R3i로 정리하고 V = i(R1+R2+R3)로 정리 할 수 있다.
따라서 i = V / (R1 + R2 + R3)를 알수 있고, Rt를 저항을 합친 수라고 하면 R1 + R2 + R3 = Rt,
즉, 우리는 그림 1에 대한 등가 회로를 얻을 수 있다.

따라서 그림1과 2로부터 직렬로 연결된 저항들은 각 저항을 대수적으로 합한 하나의 등가저항으로 나타낼 수 있다는 것을 알 수 있다.
다음으로 각 저항에 분배되는 전압의 크기를 구해보겠다.
V = R1i + R2i + R3i 이 식에 i = V / (R1 + R2 + R3) 이식을 대입하면
V1 = R1 * V / (R1 + R2 + R3)
V2 = R2 * V / (R1 + R2 + R3)
V3 = R3 * V / (R1 + R2 + R3)
와 같은 식을 얻을 수 있다.
이렇게 각 저항에 분배되는 전압은 각 저항에 비례하여 분배된다는 것을 알 수 있다.
우리는 저항 3개를 가지고 했지만 저항을 N개로 해도 식은 변함없고, 저항만 추가 될 것이다.
이해가 잘 안되었는가? 백문이 불여일견, 바로 예제로 실습해보자

위 회로에서 Vo와 Io를 저항 R과 Vs의 함수로 표현하라.
정답은 Vo는 (1/5)Vs, Io는 (1/5R)Vs
문제에 대해 풀이를 적어보겠다.

허접해도 이해바란다.. 최대한 풀어서 작성해보았다.
직, 병렬 회로를 합치면서 등가회로를 만들어 주었다.
저렇게 하면 회로에 흐르는 전류를 알 수 있다.
Vs 와 (5/8)R을 활용하여 It를 구해보겠다.
Vs / (5/8)R = It가 된다. 그럼 이제 Io를 구해보겠다.
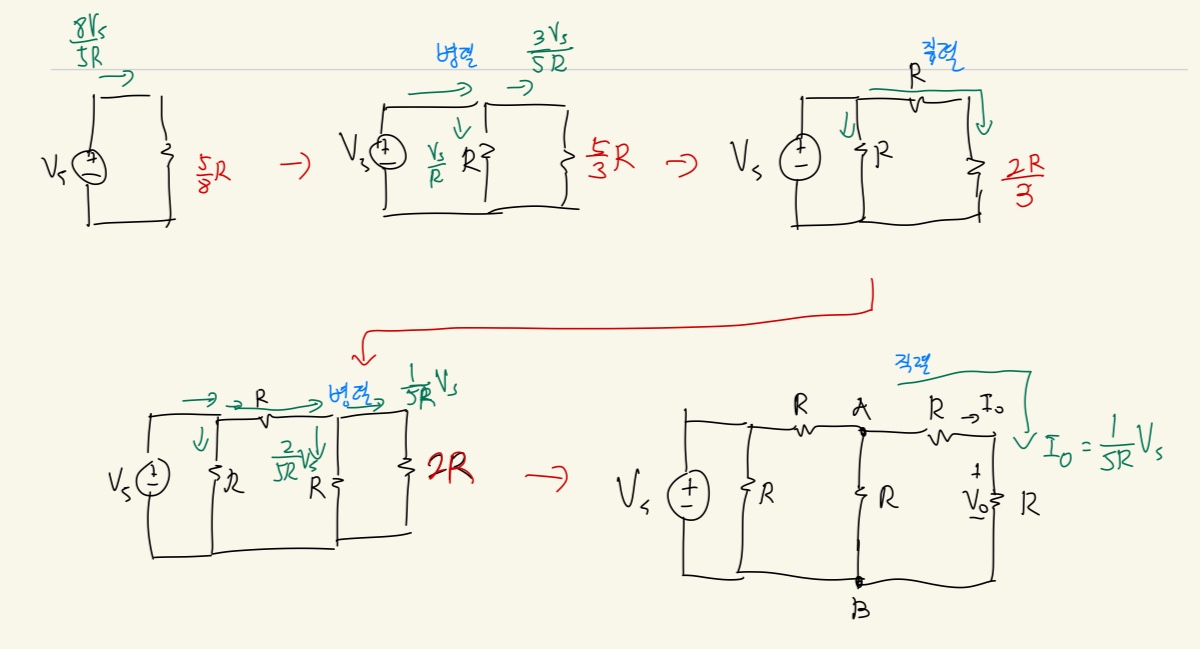
It를 활용하여 위 그림에 따라 직, 병렬로 전류를 분배하여 Io의 값을 구할 수 있다.
그럼 Io는 Vs/5R임을 알 수 있고, 여기서 Vo를 구하기는 쉽다.
옴의 법칙을 사용하면 Vs / Vs/5R = Vs/5을 얻을 수 있다.
사실 앞서 배운 전압 분배의 원리로 풀면 더 쉽게 풀 수 있다. 위 풀이들은 이런 방법으로 이해를 돕는다 라고 생각하면 되고 이제부턴 필요한 부분만 풀어서 올리겠다.
저항의 병렬 연결과 전류분배
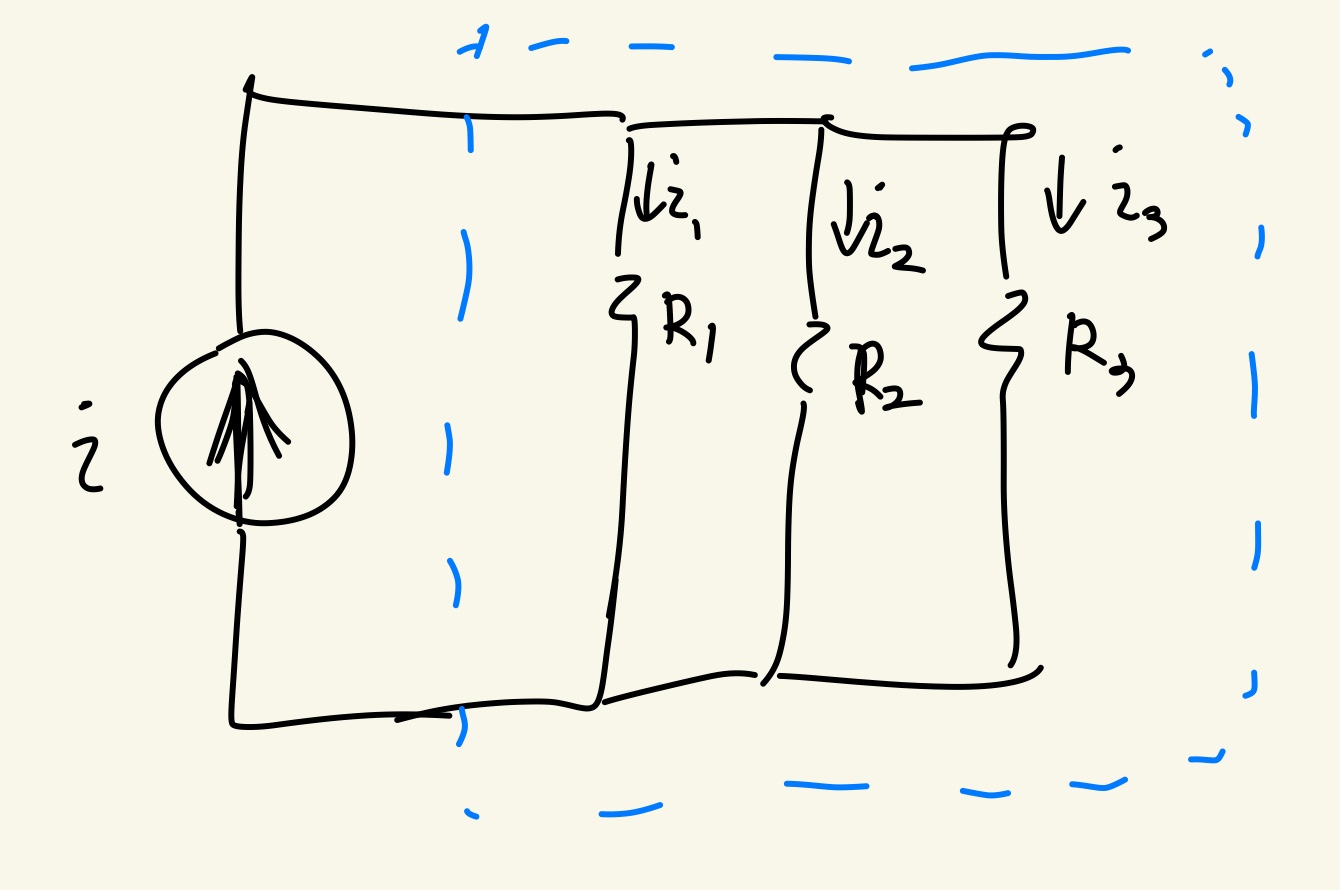
각 소자의 공통 전압을 V라고 하고, 각 저항에 흐르는 전류를 각각 i1,i2,i3라고 정의하여 키르히호프의 전류 법칙을 적용하면
i = i1 + i2 + i3
라는 식이 나온다.
우리는 전류가 어떤 비율로 분배되는 가를 알기위해 식을 풀어써보겠다.
i1 = V/R1
i2 = V/R2
i3 = V/R3
이 식을 위에랑 합치면
i = V/R1 + V/R2 + V/R3 = V ( 1/ R1 + R2 + R3)
위 식이 나오게 된다.
따라서 그림 3을 등가회로로 나타내면
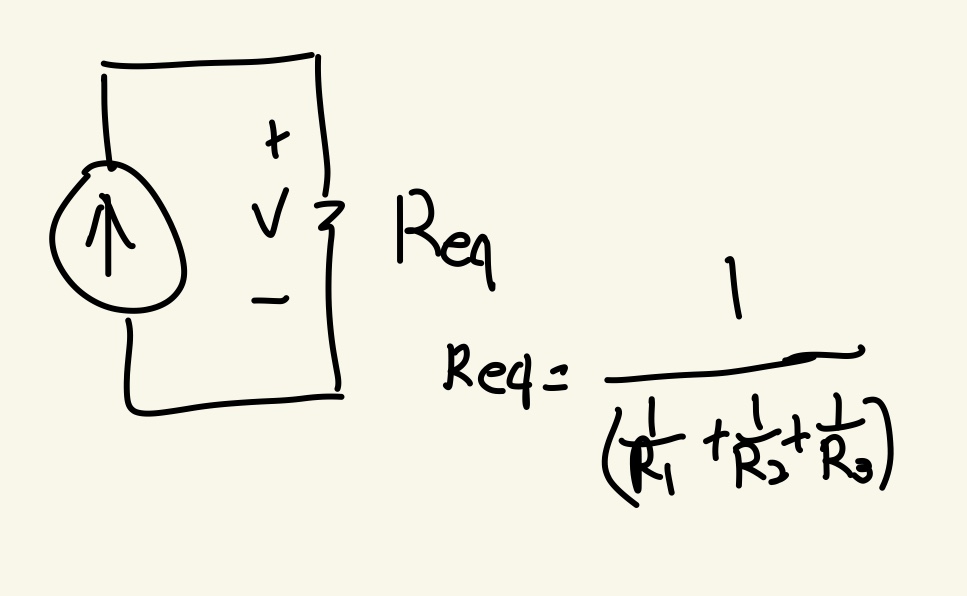
이렇게 된다.
여기서 우리는 Req를 표현하기 복잡하여 저항의 역수인 컨덕턴스를 이용하면 수학적인 표현이 간단해지는 걸 알 수 있다.
각 저항의 컨덕턴스를 G1, G2, G3라 가정하면 아래와 같다.
G1 = 1 / R1, G2 = 1 / R2, G3 = 1 / R3
Geq = 1 / Req = G1 + G2 + G3
이제 각 저항에 분배되는 전류의 크기를 구하면 된다.
i1 = V/R1 = G1 * V = G1 * Req * i = ( G1 / Geq ) * i
i2 = V/R2 = G1 * V = G1 * Req * i = ( G1 / Geq ) * i
i3 = V/R3 = G1 * V = G1 * Req * i = ( G1 / Geq ) * i
이로써 각 저항에 분배되는 전류는 각 저항에 대한 컨덕턴스에 비례하여 분배된다는 것을 알 수 있다.
예제 풀면서 이해를 돕도록 하자
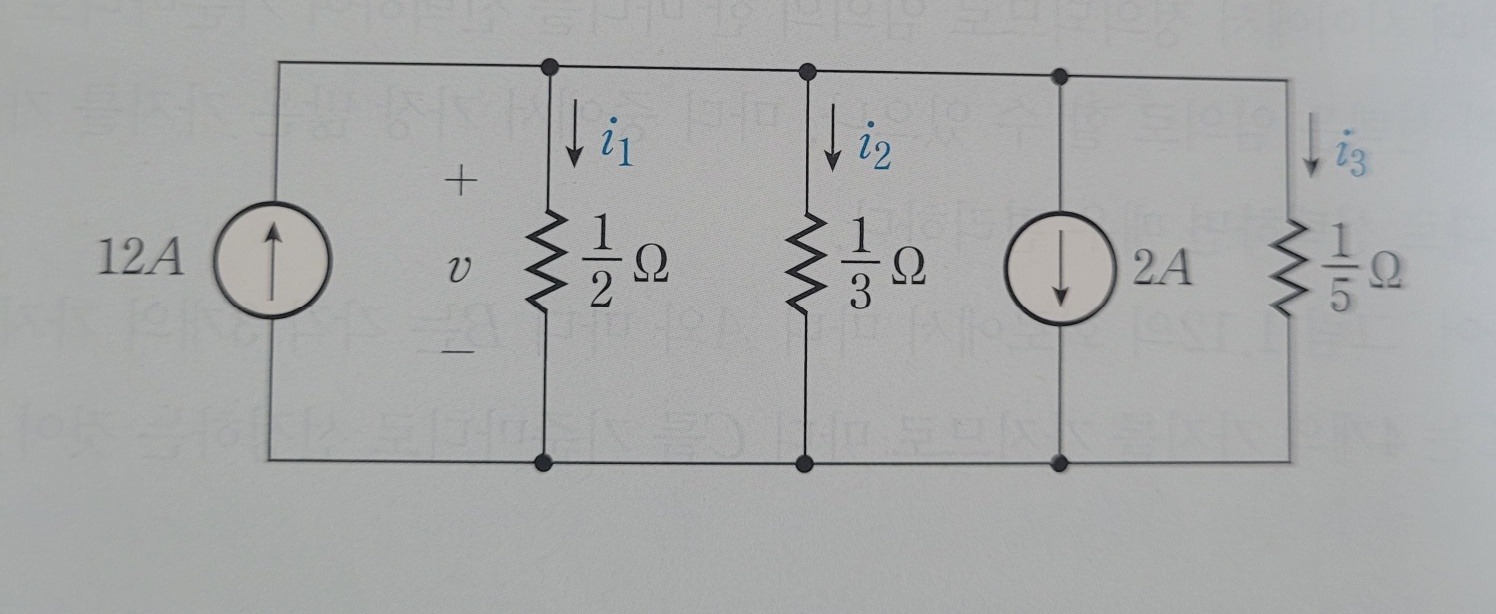
전압 V와 각 저항으로 분배되는 전류 i1, i2, i3를 구하라
정답은 V : 1V, i1 : 2A, i2 : 3A, i3 : 5A
풀이를 적어보겠다.
먼저 12A 하고 2A를 합친다.
12A - 2A ( 방향이 다르므로 ) = 10A가 된다.
그럼 총 i1, i2, i3로 전류가 나뉠텐데, 우리는 분배하는 법을 배웠다.
Geq = 10모이고, G1 = 2모, G2 = 3모, G3= 5모가 된다.
따라서
i1 = 10 * Geq * G1 = 2A
i2 = 10 * Geq * G2 = 3A
i3 = 10 * Geq * G3 = 5A
가 되고, V는 2 * 1/2이니 1V가 된다.
생각보다 쉽지 않은가?
이렇게 저항의 직렬, 병렬연결 과 전압, 전류 분배가 끝이 났다.
다음 포스터는 마디 해석법이다.
'기초전자회로' 카테고리의 다른 글
| 중첩의 원리 (0) | 2024.09.29 |
|---|---|
| 메쉬해석법 (1) | 2024.09.27 |
| 마디해석법 (0) | 2024.09.24 |
| 키르히호프의 전류, 전압 법칙 (3) | 2024.09.22 |
| 전기회로 기초이론 (1) (0) | 2024.09.21 |