테브난 정리를 알았으니 이제 노턴 정리에 대해 알아보자
노턴 정리

위 그림에서 복잡한 회로를 전기적으로 등가가 되는 b의 점선 부분으로 대체할 수 있다면, 부하저항에 대한 전압과 전류를 쉽게 구할 수 있다.
따라서 우리는 다음 식을 얻을 수 있다
iL = ( Rn / (RN + RL) ) * In
VL = RLiL = ( RL*Rn / ( Rn + RL ) ) * In
테브난 정리와 같이 특정 부분에 대한 해석을 신속하게 계산할 수 있다.
노턴 정리를 단계로 요약해보면 다음과 같다.
1 단계 : 노턴 등가회로를 구하려는 두 단자를 개방하여 부하저항을 제거한다.
2 단계 : 두 단자를 단락시킨 후 단란전류 In을 구한다.
3 단계 : 모든 전압원은 단락시키고 모든 전류원은 개방시킨 상태에서 두 단자 사이의 등가저항 Rn (=Rth)을 구한다.
4 단계 : In과 Rn을 병렬로 연결하여 원래의 회로를 대체하는 노턴 등가회로를 구성한다.
5 단계 : 노턴 등가회로의 양단에 1단계에서 제거한 부하저항을 연결하여 부하저항에 대한 전압과 전류를 계산한다.
노턴정리의 적용 예를 보자

먼저 단자 A, B를 단락 시킨다음 두 단자 사이에 흐르는 단락전류 In을 구해보자

iT를 구하고 In, Rn을 구하는 방법은 다음과 같다

Rn이 왜 저렇게 나오는지 궁금할 텐데 In을 바라보는 방향으로 계산해야한다. (테브난 Rth와 같다)

그럼 노턴정리에 의해 저렇게 등가회로가 만들어지고 우리는 VL과 iL을 구할 수 있다
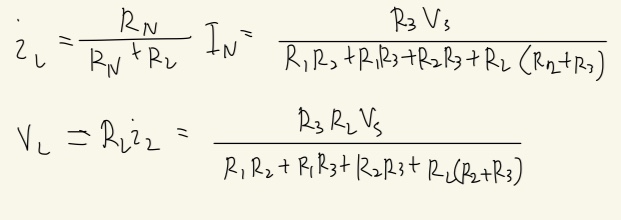

위 회로를 프로그램을 통해 돌려보니 잘 나온거 같다. ( 다시 말하지만 1.16666...이기 때문에 반올림하여 1.2A, 1.2V가 된거다 )
이해의 부스터를 달아주기 위해 예시를 살펴보자

Vo와 Io를 구하자
정답은 Vo = 7/6V, Io = 7/6A이다
풀이를 보도록 하자

먼저 중첩의 원리를 적용하여 In의 값을 구해준다

그리고 Rn을 구하기 위해 1옴 양단을 개방하고 전원을 차단하면 위와 같은 식을 얻어 Rn의 저항을 알수 있다

그리고 노턴 등가회로를 그려주고 Vo와 Io의 값을 그려주면 된다.
문제를 풀어보니 별거 없지 않은가?
다음은 연습 문제들을 가져와서 풀이를 해보겠다.
이제껏 배운것들을 전부 적용하여 풀어보자!